Let’s Play Fair: A Deceptively Simple Cipher

By Nathan Dumessa (Guest Contributor)

What is the best way to keep your secret messages safe? Using a cipher that is deceptively simple. This is what makes the Playfair cipher stand out among the other ciphers.

Charles Wheatstone may be more famous for his contributions to the invention of the telegraph, but what some may not know is that he invented the Playfair cipher, which he named after his friend, Lyon Playfair. Wheatstone was also an important figure in the study of vision. He made a revolutionary contribution with his invention of the stereoscope in 1838 (Banerjee, 2014). This was one of his greatest inventions that led to his popularity. In addition, his work on the telegraph may have led to the creation of the Playfair cipher. After all, the invention of the telegraph was a game-changer in the world of cryptography.

One of the most famous uses of the Playfair Cipher involved John F. Kennedy during World War II (Lyons, n.d.). He was able to send a message encrypted using this cipher when his PT-109 sank in the Solomon Islands and managed to get his crew and himself rescued.

What I really admire about this cipher is how simple it can seem, but is actually difficult to decipher. The structure of the Playfair cipher is a 5×5 grid of the English alphabet. This will of course exclude a letter, but in this cipher, the letters I and J are combined to represent one letter. Similar to the Keyword Cipher, the Playfair cipher also uses a keyword. The rules for the keyword apply here as well with the addition of one new rule: If any letter is repeated in the key, it is eliminated, the entire grid has to contain all of the letters except for J since it is represented by the letter I, and finally the key cannot contain the letters J and I.

The next step to setting up this cipher is to split up your message into two-letter pairs called digraphs. When doing this, you have to disregard all punctuation and write out any numbers that may be included. Now there are a few restrictions that apply here: Any double letters are separated by the letter X, and if you have an odd number of letters in your message, you add an extra X at the end to make it even, for example, the word BELL would be written as BE LX LX. Now the only thing left is to encrypt the message. So for this example our sentence will be HE RANG THE BELL AT SEVEN PM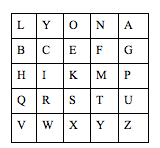

The sentence would then be broken apart into: HERANGTHEBELLATSEVENPM

HE RA NG TH EB EL LA TS EV EN PM

Note that it was not necessary to put an X between the two L’s in the word BELL because they were in two separate digraphs.

The encryption process has a specific algorithm. For our example, we will use the keyword LYON and set up a grid first.

Now to encrypt our message, we will look at each pair of letters at a time.

HE RA NG TH EB EL LA TS EV EN PM

The way you encrypt each pair is by looking at their locations in the grid, so HE forms a 2×3 rectangle. You start by looking at the H and following it to the E column and you get the letter K. Then you follow the E left to the H column and you get the letter B. So the first pair will be encrypted to KB.

If two letters are located in the same row, you would shift one position to the right. For example, if you are trying to encrypt the letters IM, it would be translated to KP. If the letters are in the same row and in the first or last columns for example LA, you would translate it to YL. Similarly, if two letters are in the same column, you would shift down one position so the letters AP for example, would be encrypted to GU, and following the same pattern, CW would be translated to IY.

So our message would be encrypted to:

HE RA NG TH EB EL LA TS EV EN PM

KB UY AF QM FC BO YL UT BX FO HP

Or: KBUYAFQMFCBOYLUTBXFOHP

The main weakness of the Playfair cipher is the fact that the sender would have to inform the recipient of the keyword. If an enemy were to intercept this information, the message would be decrypted in a very short amount of time. However, without information on the key, cracking this cipher would prove to be a daunting task.

In attempting to cryptanalyze a message like this, one would first need to figure out whether or not it is a Playfair cipher. The important characteristics are: an even number of letters, no double letters, and if it’s a long message, a frequency analysis that shows no more than 25 letters. Once that is done, most of the approach involves a trial and error method. Contextual evidence would help because it would provide some plausible guesses. Because the cipher is digraphic, substituting a pair of letters at a time, frequency analysis would not be an efficient method to decipher it. Therefore, a cryptanalyst would have to use a different approach to crack this cipher. One thing to consider is that in this cipher, reversed plaintext digraphs correspond to reversed cipher text digraphs, so that would help pick out a few letters.

The Playfair cipher was actually used in World War II by the German army, but instead of using the regular cipher, they used a double Playfair which eliminated the weaknesses in the cipher (Christensen, 2006). In the double Playfair, the first letter of the digraph would be in one grid and the second would be in the other. Therefore, reversed plaintext digraphs would not actually correspond to reversed cipher text digraphs. In addition, double letters could be present in the cipher text which can give a false pattern to a cryptanalyst.

The Playfair cipher is one that is very simple to utilize but time consuming and difficult to decipher. The main weakness is how easy it is to crack it if someone knows the keyword. Otherwise, it is one of the best ciphers to securely encrypt a message as long as your intended recipient knows the key. It is important to note that the keyword is vital. The security of the message depends on the mutual understanding of the key between the sender and recipient and as little written evidence of it as possible.

I will leave you with this:

TAZSQVRMIPPBLMDQDYRIRFEPDATAQLMCRCPQAFTAFAVAMIIDLMALEOIMERVTHFSVKZ

This post is part of a series of essays on the history of cryptography produced by students at Vanderbilt University in honor of the release of The Imitation Game, a major motion picture about the life of British codebreaker and mathematician Alan Turing. The students wrote these essays for an assignment in a first-year writing seminar taught by mathematics instructor Derek Bruff.  For more information on the cryptography seminar, see the course blog.  And for more information on The Imitation Game, which opens in the US on November 28, 2014, see the film’s website.

Sources:

Akins, T. Playfair Cipher. (n.d.). Retrieved October 15, 2014. http://rumkin.com/tools/cipher/playfair.php.

Banerjee, J. (2014, August 15). Charles Wheatstone (1802-1875). Retrieved October 15, 2014. http://www.victorianweb.org/technology/inventors/wheatstone.html

Christensen, C. (2006, January 1). Playfair Cipher. Retrieved October 15, 2014. http://www.nku.edu/~christensen/section%2019%20playfair%20cipher.pdf

Lyons, J. Playfair Cipher. (n.d.). Retrieved October 15, 2014. http://practicalcryptography.com/ciphers/playfair-cipher/